[딥러닝의 통계적이해] 딥러닝과 통계학
오늘 배우는 목록 ~~ 퍼셉트론과 아달린, 선형 회귀모형, 로지스틱 회귀모형, 경사하강법 ~~ 이걸 한 강의만에~~?

통계학
데이터(경험)을 통해 배우는 과학
통계적 추론 : 적은 데이터로 모집단 일반화
답이 있는 데이터가 많아지고 컴퓨팅 능력 향상 -> 알고리즘 기반 머신러닝
| 통계학 | 딥러닝, 머신러닝 |
| 모수 parameter | 가중치 weights |
| 추정 estimation , 적합 fitting | 학습 learning |
| 회귀 , 분류 | 지도학습 |
| 군집화, 분포 추정 | 비지도학습 |
| 독립 변수 , 설명 변수 | 특징 |
| 종속 변수 , 반응 변수 | 레이블 |
통계모형 : X 면 Y 다 라는 인과구조를 찾는 것이 목적, Y=a + bX + error 에서 a, b 를 알아내는 것
딥러닝 모형 : 블랙박스 -> 결과 예측 목적
| 전통적 통계모형 | 딥러닝 모형 | |
| 데이터 크기 | 소규모 | 대규모 |
| 모형의 구조 | 데이터 = 생성구조 + error | error가 주 문제 아님 |
| 모형의 크기 | 데이터 생성구조를 저차원 모형으로 파악 | 데이터 생성구조 복잡 - 고차원 모형(블랙박스) |
| 모형의 평가 | 적합도, 유의성 | 예측력 |
| 모형의 작성 | 생성구조를 오차에서 분리 | 학습을 통해 데이터 복잡성 이해 |
확률 probability : 사건이 일어날 가능성. 0~1 사이 숫자로 표현
사건 B의 정보량 : I(B) = -log[P(B)]
P(B) : B가 일어날 확률
확률변수 : 표본공간의 특정 사건을 숫자로 바꿔주는 함수, 이산형 확률변수와 연속형 확률변수
분포를 알아볼 수 있는 것 -> 기댓값과 산포
기댓값

엔트로피
정보량의 기댓값
불확실성 지표
- X가 이산형인 경우, 확률질량함수

2. X가 연속형인 경우, 확률밀도함수

베르누이 분포
시행 결과가 둘 중 하나인 것
동전 던지기
X ~ Ber(p)
분류가 2개로 되는 머신러닝에 활용
확률질량함수

멀티누이 분포
확률변수가 K개 범주일 때
주사위 던지기

정규 분포
연속형 변수 예측에 활용

퍼셉트론과 아달린
- 초기 신경망 모형
- 오차수정법으로 학습
퍼셉트론
1958년 로젠블랫 이미지 인식 기계인 퍼셉트론 개발
선형이진 분류기 binary

1949년 헵 학습 규칙
- 시냅스가 약간 떨어져서 이어져있는데 시냅스가 흥분하면 연결된다 : 시냅스의 가소성
퍼셉트론은 손실함수없이 학습한다
가중치 값을 구한다
오차로 가중치 갱신
아달린
손실함수 정의

오차가 클수록, 입력값이 클수록 가중치가 많이 바뀜
선형 회귀모형
경사하강법으로 추정가능
최소제곱법
y_hat = w0 + w1x1 + error 에서 w0과 w1을 구하는 것이다.

최대가능도법
가능도 함수를 최대화하는 w0, w1 가중치를 구한다.
최대가능도법 추정결과 == 최소제곱법 추정결과
최적화 방법
머신러닝 == 최적화 optimization 문제
뉴턴의 방법, 경사하강법
뉴턴의 방법
f(x)=0 을 만족하는 x를 찾는다
f(x)를 미분해나가는게 0을 찾을 확률이 높다.
(J'(w)=0 손실함수 값을 찾는 것, J''(w) 미분 두번한거 )
w := w - J'(w)/J''(w)
J(w) 2차 미분 가능 함수여야 함, 변수 수가 적어야 함
볼록함수에 좋다
경사하강법
손실함수의 대표적인 방법
현재 함수 위치에서 조금씩 이동해서 최솟값으로 (조금씩 가중치 갱신)

작은 학습률 : 오래걸릴 수 있음
큰 학습률 : 빨리되나 최저점을 못가고 맴돌수 있음
-> 처음에는 크게 학습하고 나중에 학습률을 줄여나감
확률적 경사하강법 SGD
데이터 100개 중 하나씩 사용
많이 돌아서 복잡하게 갈 수 있다
미니배치 경사하강법 (일부 데이터 이용)
epoch
전체 데이터를 학습하는 횟수
1 epoch : 훈련 데이터 1번 전체 학습
로지스틱 회귀모형
output : 2개 범주 -> 확률값으로 표현하는게 좋음 ( 0.5보다 크면 1, 작으면 0 .... )
sigmoid 함수 - 활성화 함수

가능도 함수를 최대화하는 가중치 : 로그가능도 함수
로그가능도 함수를 미분해서 최대화하는 w를 구하는 법 - 경사하강법
로그가능도 함수 최대화 = 손실함수 최소화
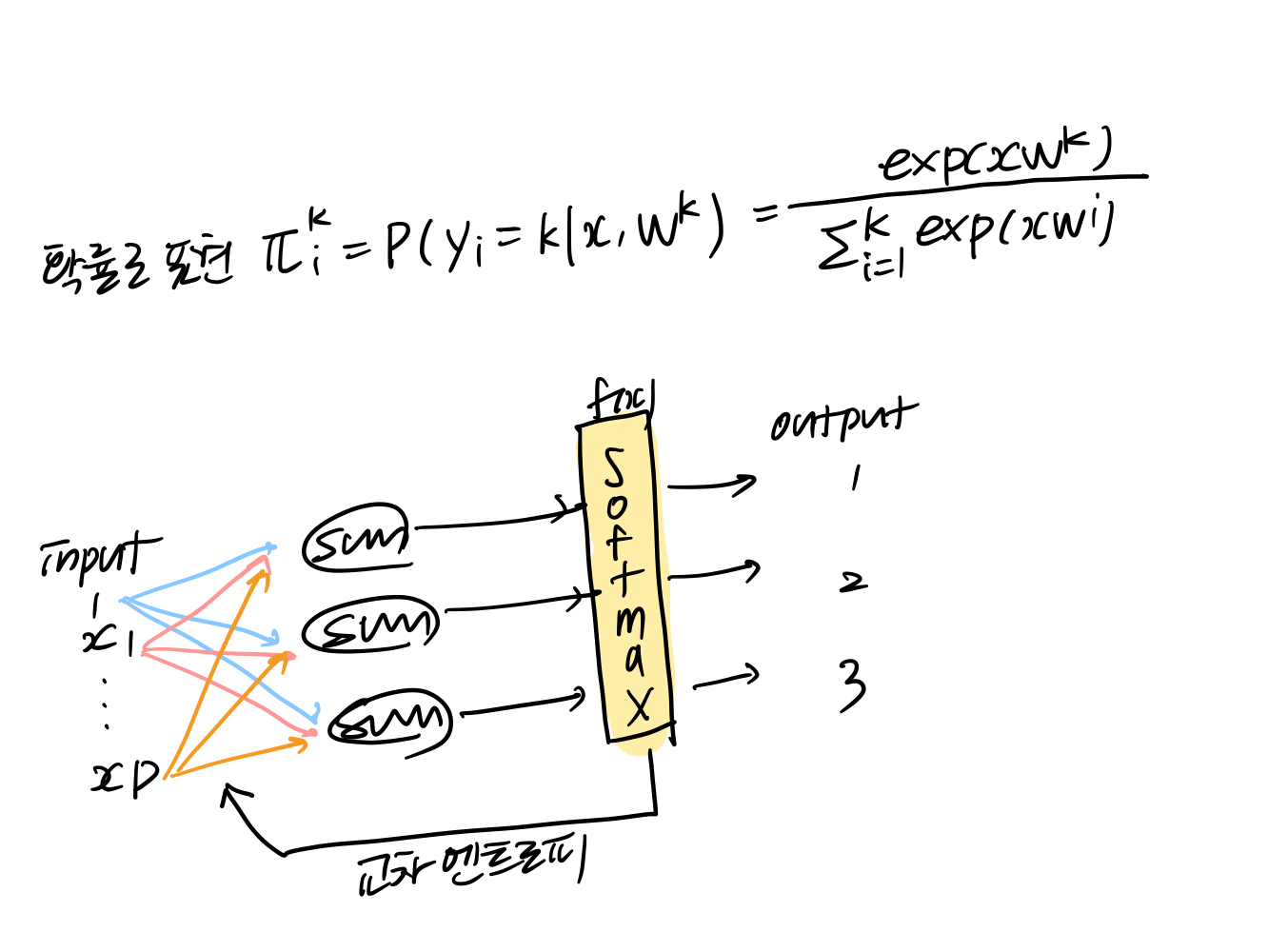
소프트맥스 회귀모형
output : 여러개 범주
softmax 함수 -활성화 함수
경사하강법으로 추정 가능
XOR 문제와 다층 신경망
XOR 문제
민스키와 페퍼트 : 퍼셉트론(1개 층 신경망)은 선형적 분류만 되고 XOR 문제를 해결 못한다
XOR문제를 아래와 같이 해결가능하겠다...!
