표본분포 알아내는 방법 (약대수의 법칙, t분포)

모집단 : 관심의 대상이 되는 전체

표본 : 모집단의 일부

표본분포 : 표본을 이용한 통계량의 확률분포

대수의 법칙 : 표본 수가 커지면 표본 평균이 모집단의 평균에 수렴한다는 법칙

t 분포 : 표본 수가 작을 때 따르는 분포 (모집단은 정규분포를 따른다)

 

모수 parameter : 알고 싶은 모집단의 특성값, 미지의 상수

통계량 statistic : 모집단의 모수를 구체적인 값으로 추정하기 위한 표본의 함수

확률 변수 : 표본에서 어떤 값이 뽑힐지 모른다는 것

표본의 함수(표본 평균, 표본 분산) = 통계량도 확률 분포를 가짐 (표본이 늘 같을 수 없기에)

 

표집분포

랜덤표본 random sample

• 관심의 대상이 되는 모집단에서 랜덤하게 추출된 일부
• 서로 독립
• 동일한 분포 따름

표본추출변동 sampling variability

• 동일한 모집단에서 추출된 표본에서 구한 표본평균 등이 달라지는 현상
• 표본추출변동 줄여야함 -> 표본을 크게 늘리게 됨

x̄ 의 표본분포 또는 표집분포

이산형 확률분포

공정한 주사위의 기대값 E(X1) = 1x1/6 + 2x 1/6 + 3 x 1/6 + 5 x 1/6 + 6 x 1/6 = 21/6 = 7/2

Var(X1) = E(X1^2) - (E(X1))^2 = 1/6x(1^2 + 2^2 + ... + 6^2) - (7/2)^2 = 35/12

 

결합확률분포, 결합질량함수

 

문제 예제 1)

평균 10, 분산 100인 모집단에서

100개의 표본을 임의로 뽑았을 때 표본 평균의 기댓값과 분산은?

E(x̄) = 10, Var(x̄) = 1/n * Var(x̄1) = 100/100 = 1

 

10000개의 표본을 임의로 뽑았을 때 표본 평균의 기댓값과 분산은?

E(x̄)=10,

Var(x̄) = 100/10000 = 0.01 -> 표본이 커질수록 0이 된다. 수렴한다 .. => 약대수의 법칙

모집단의 확률 변수가 정규분포를 따를 때 표본평균은 수정된 정규분포를 따른다!

약대수의 법칙

x̄가 모집단으로 간다. 

 

x̄ 분포

예) 가구 소득 평균 300만원, 분산 144^2만원인 정규분포

9가구 평균소득의 기댓값은? 300만원

9가구 평균 소득의 분산은? 

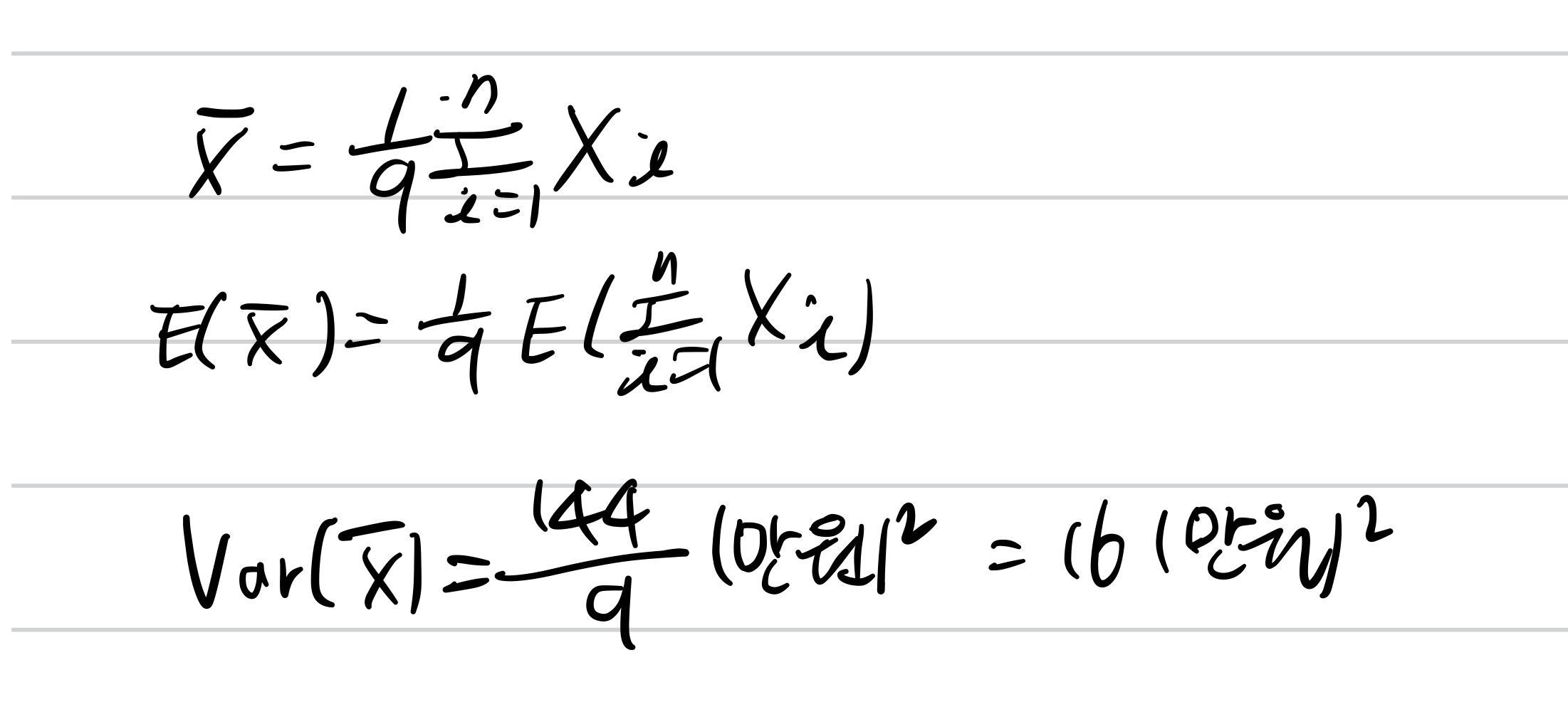
t분포

표본분산 s

정규분포를 따르는 모집단의 분산을 모를 때 표본평균은 t분포를 따른다.

 

 

연습문제)

모집단이 평균 5, 분산 100인 정규분포. 25개의 표본을 추출하고 표본평균을 구했다.

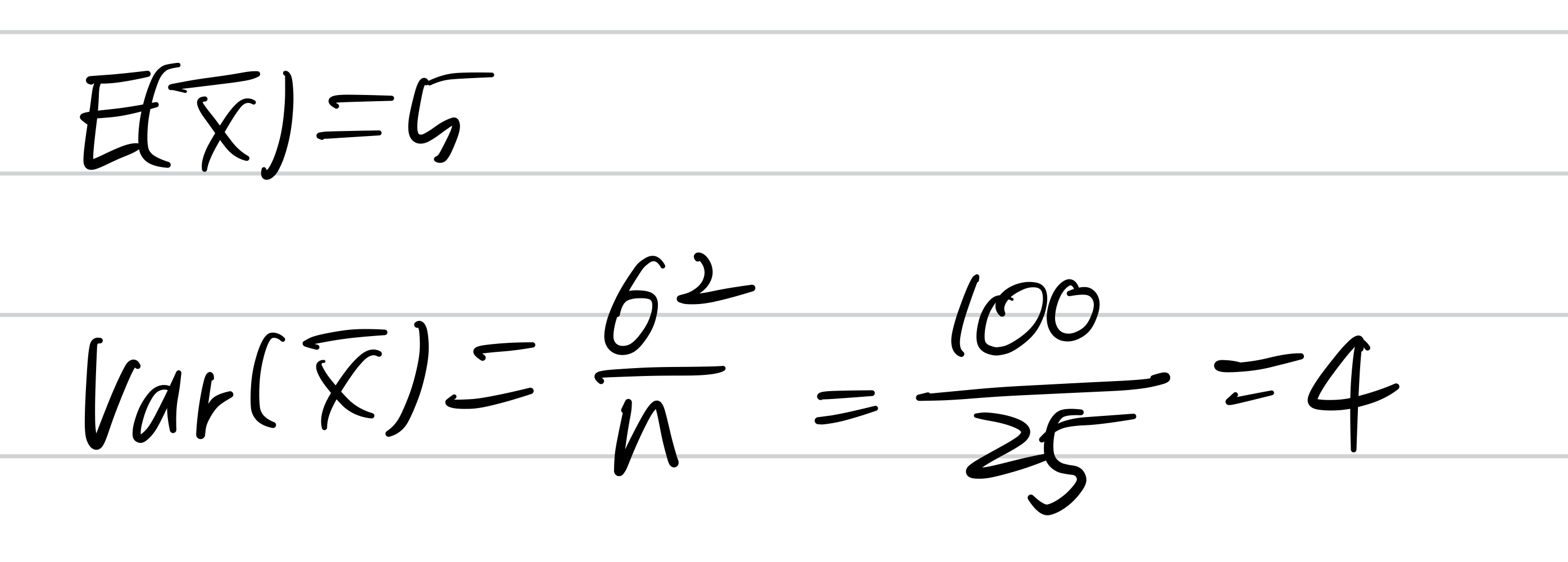
어느 도시의 가구 소득은 평균 200만원, 분산 144만원^2인 정규분포 N(200,144)를 따른다고 하자.

이 도시에서 9가구를 무작위로 뽑아서 평균소득을 구했다.

평균소득이 200만원 보다 클 확률

표본크기 n에 따라 모양이 달라진다. -> 자유도 n-1

정규모집단을 따르는 분포에서 n개의 표본을 뽑았고 student화 하게되면 자유도가 n-1인 t-분포를 따른다.

0을 중심으로 대칭인 형태

정규분포보다는 꼬리가 두터움

자유도가 커짐에 따라 점차 표준정규분포에 접근함

T.DIST(확률값이계산되는수치,분포의자유도,tails)

중심극한정리

표본크기 n이 크면 임의의 랜덤표본에 대한 표본평균의 분포는 근사적으로 정규분포를 따른다.

KESS - [통계분석] - [모의실험] - [중심극한정리]

예) 우리나라 성인남자의 키는 µ=168, σ=3 일 때, 성인남자 36명을 랜덤 추출하여 키를 조사할 때 표본평균 x̄가 169 이상일 확률은?

이항분포의 정규근사

n이 충분히 크면 이항분포의 확률을 정규분포를 통해 계산할 수 있다.

 

표본분산의 분포

카이제곱분포