[회귀모형]단순회귀모형
회귀분석 관련 변수들
- 독립변수 independent variable, 설명변수 explanatory variable : 다른 변수에 영향을 줌, 보통 X로 표시
- 종속변수 dependent variable, 반응변수 response variable : 다른 변수에 영향을 받음, 보통 Y로 표시
예시)
(한 나라에서 국민소득이 증가 -> 자동차 보유대수 증가)
(국민소득 == 독립변수, 자동차 보유대수 == 종속변수)
회귀분석 regression analysis
독립변수와 종속변수간의 함수관계를 규명하는 통계적 분석방법
영국의 우생학자 갈튼이 회귀란 용어를 처음 사용
단순회귀모형
회귀모형 중 가장 간단하다.
X 독립변수가 하나이고 선형인 것.
y=ß0+ß1x+error
ß0 : 절편 회귀계수
ß1 : 기울기 회귀계수
error : i번째 측정된 y의 오차항, 평균=0, 분산 ∂^2(제곱) - (오차항의 분산은 등분산 ∂^2으로 가정하므로)
(기능이 좋을 수록 분산의 수는 작다)
두 변수의 모형을 알고자 한다 -> X, Y 축으로 높고 그래프를 알아야 한다. -> 산점도를 그려본다.
산점도 scatterplot
R studio를 이용해서 scatterplot을 그릴 수 있다.
x, y 축을 정하면된다.
plot(x_data, y_data, xlab="x_label", ylab="y_label", pch=19)산점도 그래프 결과 비례 관계로 데이터가 분포하는 것을 확인 -> 이를 이용해 회귀직선을 구할 수 있다! X, Y 관계 추측 가능
y=ß0+ß1x+error
y 변수 = 상수항 + 오차항(확률변수)
=> y 변수는 확률변수이다.
앞서 봤듯이 오차항 error 의 펑균은 0, 분산은 ∂^2(제곱). => Y의 평균 : E(ß0+ß1x+error) = ß0+ß1x + E(error) = ß0+ß1x
error의 분산은 각 관찰점마다 분산이 같은 등분산으로 가정한다.
따라서 Y의 분산도 Var(Y) = Var(ß0+ß1x+error) = Var(Error) = ∂^2(제곱)
Y의 오차항 error들은 서로 독립이라고 가정한다. 그러면 두 변수간은 공분산 Cov(Error i , Error j)=0 이다.
E i, E j 가 서로 독립 -> 반응변수 Y i, Y j 도 서로 독립
- 대체모형 alternative model
Y i = ß0+ß1x+error i
= (ß0+ß1x의 평균) + ß1(x i - x의 평균) + error i
= ß0+ß1(x i - x의 평균) + error i
= 절편항 + 기울기항 + 오차항
여기서 계수들을 추정할 수 있어야 한다 -> 어떻게 추정하는가? 회귀선의 추정
회귀선의 추정
Y^(y hat)=ß0+ß1X : 추정된 회귀직선, 회귀선
- ß0 : X=0 일 때, Y^의 값으로 추정된 회귀절편Intercept
- ß1 : X가 X+1 할 때, Y^의 증가량. 기울기 slope
ß_0, ß_1 구하자.
1. 최소제곱법
error(i) = Y(i) -ß0 - ß1X(i) 에서 오차제곱들의 합 S (i 번째)
S = ∑ error(i)^2
S (오차제곱들의 합)를 최소로 하는 ß0, ß1를 추정.
편미분
오차제곱합을 최소화하는 것을 구하기 위해 ß0, ß1를 각각 편미분할 수 있다.

이를 정규방정식 normal equations 라고 부른다.
이러한 식들은 그래프를 그려보면 더 이해하기 쉽다.

이를 R studio에서 하나하나 하기보다는... lm 이라는 함수를 사용할 수 있다.
market.lm = lm(Y ~ X, data=market)
summary(market.lm) # 결과summary 는 다양한 결과를 보여주는데 그 중 Coefficients에서
y 절편은 0.3282이고 x에 대한 기울기가 2.1497임을 알 수 있다.
추정된 회귀식을 세울 수 있다.
y^= 0.3282 + 2.1497x

앞서 배운것들을 활용한 예시를 보자.
산점도 위에 회귀선을 덧붙일 수 있다.
plot(market$X, market$Y, xlab="광고료", ylab="총판매액", pch=19)
title("광고료와 판매액의 산점도")
abline(market.lm) # 앞서 구해둔 회귀선을 그린다
identify(market$X, market$Y) # 마우스를 관심있는 관찰값을 누르면 값을 볼 수 있다.identify를 이용하여 관심있는 값을 확인할 수 있다.
잔차(residual)

names(market.lm) # market.lm의 변수명들 : names
resld = market.lm$residuals
fitted = market.lm$fitted
sum(resid) # 잔차들의 합
sum(fitted) # 예측값의 합
sum(market$Y) # 관찰값의 합
# 관찰값 Y의 합과 추정값 Y^의 합이 같다.
회귀선상에 점이 있는지 확인해보자.
points와 text, locator 기능을 확인하자.
text(locator(1), y=ax+b) 에서 locator(1)는 마우스가 위치하면 출력해주는 기능이다.
plot(market$X, market$Y, xlab="광고료", ylab="총판매액", pch=19)
title("광고료와 판매액의 산점도")
abline(market.lm) # 회귀선을 그리고
xbar = mean(market$X)
ybar = mean(market$Y)
points(xbar, ybar, pch=17, cex=2.0, col="RED")
# x,y값의 평균값 점을 찍어보면, xbar, ybar는 회귀선상에 있다. 를 알 수 있다.회귀모형의 정도
해당 회귀선의 유의성을 확인하기 위해서 분산분석표를 확인해야한다.

제곱의 합은 자유도를 갖게된다.
회귀식을 주면 반드시 분산분석표를 제공해야한다.
분산분석표를 이용해서... anova
- 가설검정 : 기울기가 0인가 아닌가 (F0-검정통계량 값을 이용한다)
- 검정방법 : " F0 > F(1, n-2)" 이면 귀무가설을 기각, 회귀직선이 유의하다라고 한다.
- R에서는 F0에 대한 유의확률로 p값이 제공된다. p값 < 유의확률 이면 귀무가설을 기각한다.
market.lm = lm(Y~X, data=market) # 적합한 회귀모형 결과
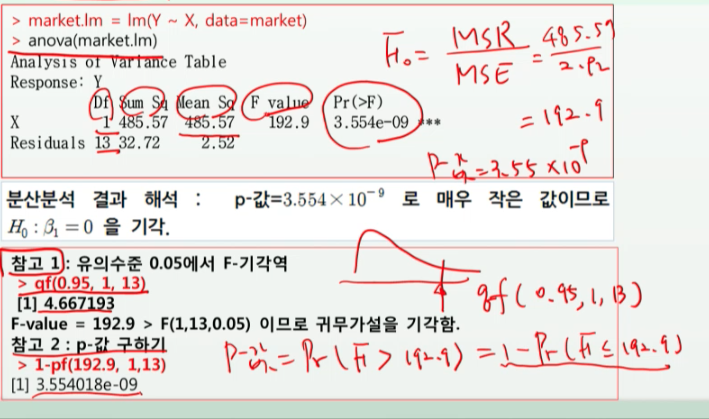
anova(market.lm) # 분산분석표 생성
Df : 자유도
Sum Sq : 제곱합
Mean Sq : 평균 제곱
F value
Pr : 유의확률
분산분석표 결과 해석 : Pr값이 매우 작은 경우, H0: B1=0을 기각한다.

(이부분을 잘 모르겠다.)
결정계수 Multiple R-squared
총변동을 설명하는데 있어서 회귀선이 변동을 얼마나 잘 설명할 수 있는가 : 회귀선의 기여율!
결정계수 R^2 = 회귀제곱합 SSR / 총변동중 SST

anova 분산분석표를 보면, Sum sq(제곱합)이 X에 대한 것과 Residuals(잔차)에 대한 것이 나와 있다.
여기서, SSR/SST -> X에대한것 / (X에 대한것 + 잔차에 대한 것) . 만약 0.94라면 94프로 설명할 수 있으므로 유의하다고 해석이 가능하다.
추정값의 표준오차
이를 이용해서도 판단이 가능하다.
∂제곱의 불편추정량 = MSE
∂^ (∂ hat) = √MSE 추정값의 표준오차
추정값의 표준오차는 두 모형의 비교에서 이 값이 작은 모형이 주어진 자료에 더 잘 적합한다는 의미로 이용됨

회귀모형을 적용시키고 결과를 보면,
F0값과, Multiple R-squared(결정계수값), Residual standard error(추정값 표준오차)
추정값 표준오차 == error에 대한 평균 제곱근
상관계수와 결정계수 관계
상관계수 : 상관계수는 두 연속인 변수간의 선형관계가 어느 정도인가를 재는 측도

r(상관계수) = ±√R의제곱(결정계수)