여정의 기록
[베이즈데이터분석] 베이즈 추론의 배경 본문
베이즈 추론의 시작
토마스 베이즈 Thomas Bayes 1702 ~ 1761.04.17 영국 장로교 목사이자 아마추어 수학자였다.
일주일에 한 번 설교하는 게 일의 전부여서 남는 시간이 많았다고 한다.
흄 David Hume
경험론적 철학자로 유명하다고 한다. 인과관계를 인간이 파악할 수 있다는 믿음을 의심한 사람. 모든 것은 경험을 통해 배울 수 있다고 함. 흄의 논리를 따라가다 보면 신을 의심하게 했음. 흄의 책에 반박으로 베이즈가 논문(신의 존재를 증명할 수 있다)을 씀.
피에르 시몬 라플라스 Pierre-Simon Laplace
베이즈 정리 재발견 -> 원인의 확률
태양계의 안정성 문제를 확률로 다룰 수 있다 생각, 확률에 대한 연구 시작
중심극한정리 Central Limit Theorem 발견
남녀출생성비 계산
나폴레옹 : 왜 당신의 책에는 신에 대한 이야기가 없냐?
라플라스 : 나는 그 가설이 필요하지 않습니다
확률과 확률분포
확률이란?

B 가 [0,1]로 가는 함수인 P는 다음 3가지를 만족한다.
1.

함수값은 항상 0보다 크거나 같다.
2.

전체집합에서 확률값은 1이다
3. 가산 가법성을 만족한다.
가산 가법성 : B의 부분 집합으로 이루어진 집합들의 열 (B_n)이 서로소 (겹치는게 없다)일 때,
가산 : 셀 수 있다

여기서 P : 확률
X : 표본 공간 sample space
(X, B, P) : 확률 공간 probability space
X의 부분 집합 : 사건 event
조건부 확률이란?
A, B 가 X의 부분 집합이고 P(B) > 0 , B가 주어졋을 때,
- A의 조건부 확률 : P(A|B) = P(A ^ B) / P(B)
- 두개의 사건 A, B 가 -> P(A ^ B) = P(A)P(B) 이면 -> A, B 는 서로 독립임
P(A|B) = P(A^B)/P(B) = P(A) * P(B) / P(B) = P(A)
두 사건이 독립 == B가 주어졌을 때 A 확률 == A가 주어졌을 때 B 확률
A ^ B = 0 : 독립이 아님.
확률변수란?
표본공간에서 -> 실수로 가는 함수
(표본공간에서 정의된) P(x ∈ B) = (실수에서 확률 변수 x에 의해 유도된 확률분포)P_x(B)
확률분포를 표현하는 3가지 방법
1. 확률
(표본공간에서 정의) P(A)
(실수에서 정의) P(x ∈ A)
2. 누적분포함수
확률을 특징화
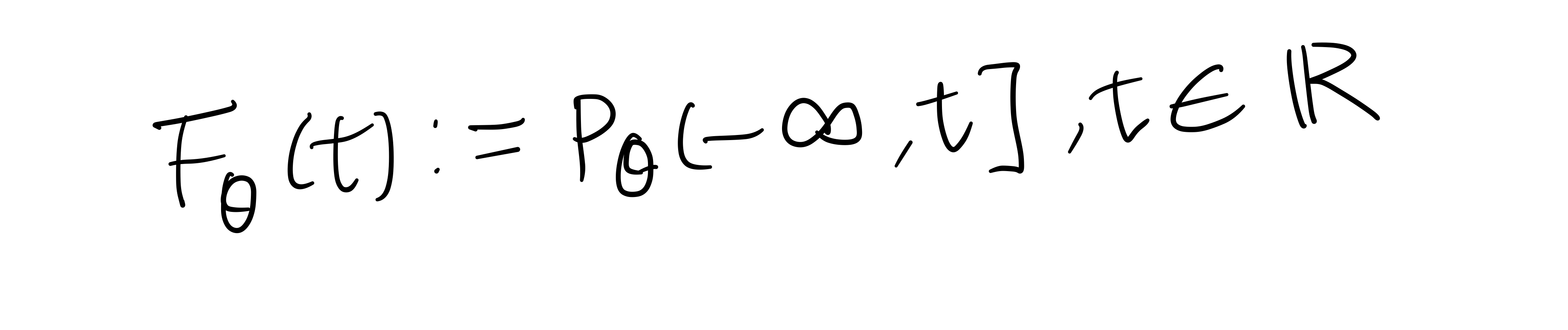
-무한대에서 t까지 확률
특징짓는다 == 누적분포함수를 정하면 확률을 알 수 있고, 확률을 알면 누적분포함수를 알 수 있다.
3. 확률밀도함수(확률을 적분으로 표현), 확률질량함수(확률을 합으로 표현)
확률밀도함수 : 확률 변수가 연속형임
확률질량함수 : 확률 변수가 이상형임


기댓값과 분산
1. 기댓값

F(dx) = f(x) dx
2. 분산
Var(x) = E(x-Ex)^2 = (평균 - 기댓값)의 제곱
'공부중 ... > 베이즈데이터분석' 카테고리의 다른 글
| [베이즈데이터분석] 베이즈추론이란? 2 (0) | 2022.12.11 |
|---|---|
| [베이즈데이터분석] 소개와 실습 (0) | 2022.08.31 |
| [베이즈데이터분석] 베이즈 추론이란? 1 (0) | 2022.08.29 |



