여정의 기록
이산형 확률분포에 대해서... 이항분포랑 포아송분포 본문
728x90
확률변수 : 확률적 실험에서 실험결과를 실수값로 대응시키는 변수
이산형, 연속형으로 구분
<이산형 분포>
이산형 확률변수의 확률분포
- 확률질량함수 pmf : P(X=x)
- 누적분포함수 cdf : P(X<=x)
확률질량함수 - 공리적 확률
조건 3가지
1. 0 <= P(A) <= 1
2. P(S) = 1
3. 배반 사건 = 공집합이 없는 경우. P(AUB) = P(A) + P(B)
겹치지 않는 사건. 시험의 합 불합격 둘 다 나올 수 없다는 것.
확률분포표
| X | 2 | 3 | SUM |
| P(X) | 1/2 | 1/2 | 1 |
1. 베르누이 시행
- 스위스 수학자 - 베르누이
- 각 시행의 결과 : 성공 / 실패 하나의 결과만 나옴
- 성공확률이 p=P(S) 라면 실패확률은 q = 1-p 가 된다
- 각 시행은 독립이다
2. 이항분포
동일한 성공확률 p를 가진 베르누이 시행을 n번 반복하여 시행시, n번 중 성공 횟수 = 확률변수 X
이항 확률변수가 특정한 x값을 가질 확률이다 ...
- X에 대한 이항분포 정의 방법과 분포함수

- 엑셀에서는 ... BINOM.DIST(성공횟수, 시행횟수, 성공률, 누적유무)
누적 -> ... 이상.. 이하.. 범위값인 경우 적용
- 기댓값과 분산
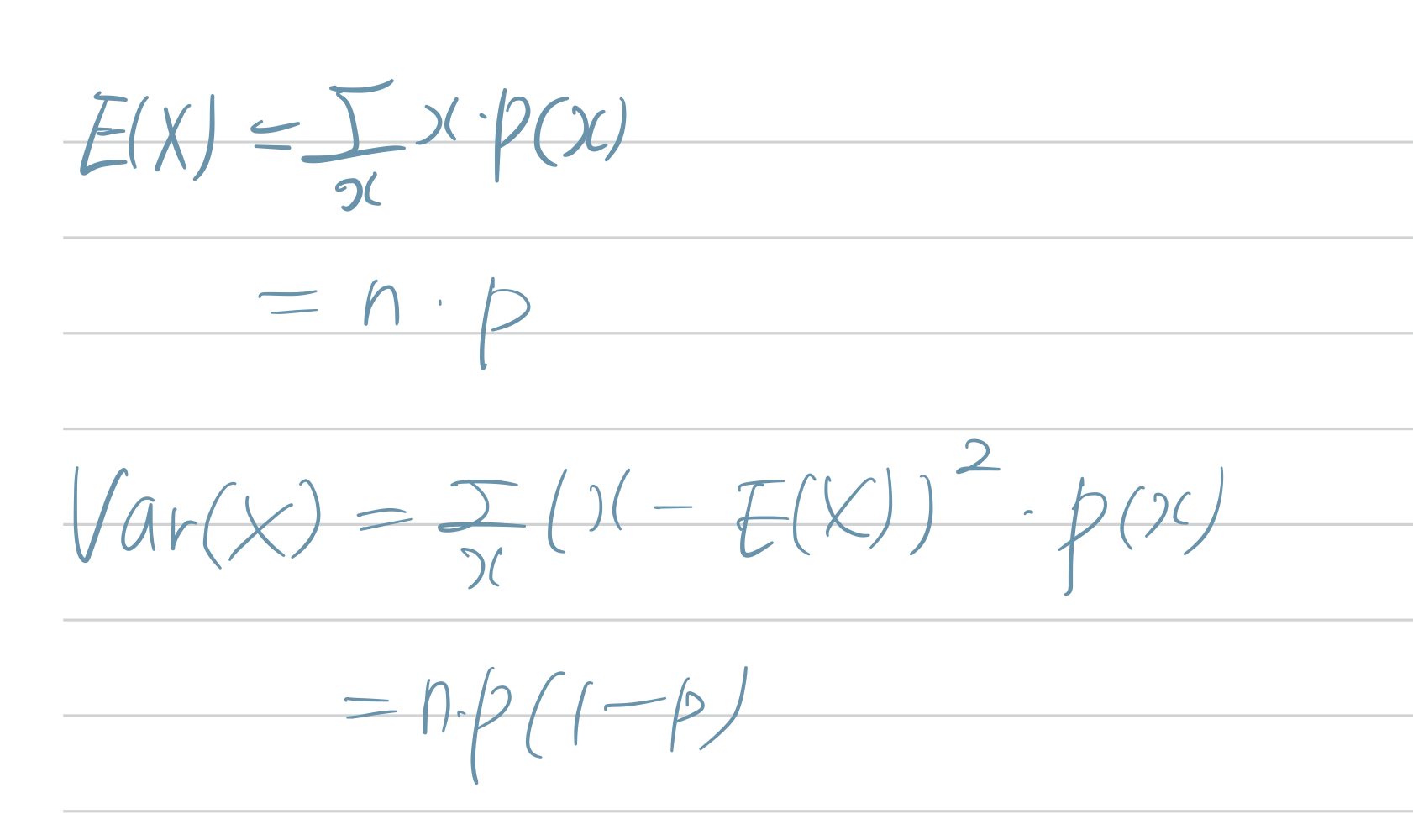
- 누적여부에 따른 분포함수
- 엑셀

- R 함수
# 특정 경우의 수에 대해
dbinom(경우의수, 총횟수, 성공확률)
# 누적의 경우
pbinom(경우의수, 총횟수, 성공확률)3. 포아송분포
한 시간동안 전화가 걸려오는 횟수(이산형) - 범위가 연속형임
하루동안 발생하는 교통사고 수
신문 1면 중 오자의 수
-> 특정 사건이 일어날 확률이 아주 작은 경우들
독립성(각 횟수는 독립), 비집략성, 비례성(범위의 증가와 횟수의 증가)
- X ~ Poisson(단위당 희귀현상의 평균 발생횟수)
X ~ Poisson(m) - 분포함수

- POISSAN.DIST(궁금한발생횟수, m, 누적여부)
- dpois(궁금한발생횟수,m)
초기하분포
전체 N개 = 1이 D개 + 0이 N-D개
728x90
'공부중 ...' 카테고리의 다른 글
| 기댓값과 분산을 알아보자 (0) | 2023.05.17 |
|---|---|
| 연속형 확률분포 continuous random variable 균등분포, 정규분포 (1) | 2023.04.25 |
| 시계열의 시간에 따른 의존관계, 자기상관 (1) | 2023.04.17 |
| 시계열의 주파수 분석과 확률과정에 대해서 (0) | 2023.04.16 |
| 시계열 데이터 R studio로 plot 그리기 (0) | 2023.04.16 |




