여정의 기록
연속형 확률분포 continuous random variable 균등분포, 정규분포 본문
728x90
연속형 확률분포 continuous random variable
어떤 구간내의 값을 취할 수 있는 확률분포
예) 집에서 회사까지 출근에 걸리는 시간을 100일 동안 수집 - 정확한 시간이란 존재하지 않으므로 ...
X = 출근 소요 시간
10 <= X <= 20 분
20 <= X <= 30 분 ...
어떤 날은 날이 안좋아서 오래 걸린다거나.. 하는 변수로 인해서 달라지는 출근 시간 ...
P(30<=X<50) 출근시간이 30분에서 50분 사이가 될 확률은? <- 이런 질문 ...
확률밀도함수
- 적분을 통해 면적을 구한다.
- f(x) >= 0
- P(X=a) = 0
- 전체면적 = 1
1. 균등분포

RAND() : 0 ~ 1 사이 난수 발생
(b-a) * RAND() + a : a ~ b 사이 난수 발생
- 분포함수

x가 a, b 사이일 때 왜 저런 값이 나오냐면 하단의 오른쪽 그래프와 같이 표현되기 때문이다.


2. 지수분포
사건발생 사이 시간의 확률분포 (/ 일정 기간 동안 사건 발생 횟수: 포아송 분포)

지수분포의 무기억성 : 과거의 일은 확률 분포와 상관없다.
3. 정규분포(가우스 분포함수) Normal distribution
- 평균을 중심으로 좌우 대칭임
- 종모양의 확률분포임
- 평균과 표준편차의 값에 의해 정규분포 모양이 결정된다
- X ~ N(평균, 표준편차 제곱)

- 분포함수

해당 분포함수 값들은 아래와 같은 정규분포 그래프에서 값을 나타내준다.

- 정규분포의 성질 68-95-99.7
뮤(평균)과 시그마(표준편차)값과 상관없이 아래의 확률이 모두 성립된다.

예시 )

- 특정값의 P(X=x) 값은 0이다. 왜냐하면 P(x)는 면접값을 나타내는데 한 지점의 면적은 항상 0이다.
그래서 P(X<=x)일때와 P(X<x)일때의 값은 같다. - 정규분포의 표준화
X ~ N(평균, 표준편차 제곱)
N(0,1) : 표준정규분포
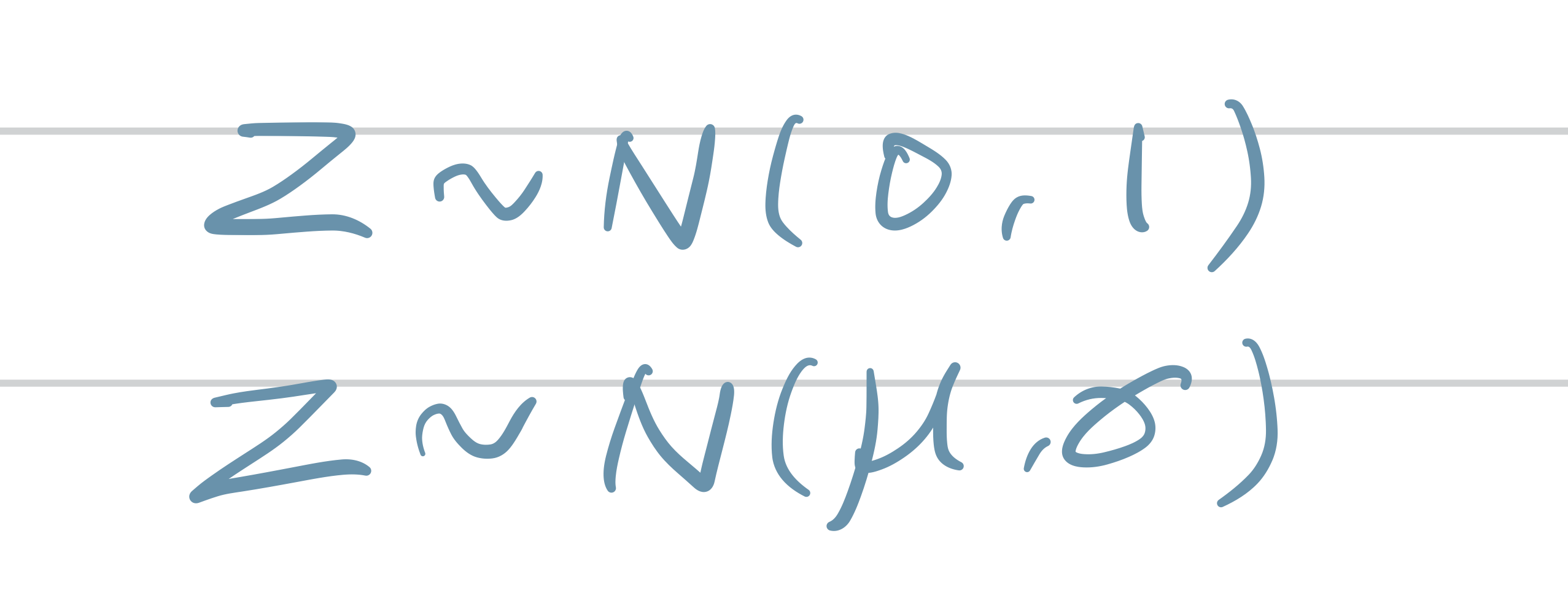


표준화를 통한 확률 계산 원래는 표준정규분포표로 계산했다

표준정규분포에서 확률계산
Z ~ N(0,1) 일 때, Z_a란?
- P(a<=Z<=b) = P(Z<=b) - P(Z<a)
- P(Z<=-a) = P(Z>=a)
- P(Z>=a) = 1-P(Z<a)

표준정규분포에서 Z_a정의
면적값이 a가 되도록하는 값을 Z_a라고 함
정규분포 엑셀함수
- NORM.DIST(확률분포를 구하려는 값, 평균, 표준편차, 누적여부)
누적이 0이면 해당x의 f(x)값 추출해줌 - 예) 통근 시간 X분 , 정규분포 N(40, 5^2) 따름, 통근시간이 50분이상 걸릴 확률은?
X='통근시간'
X ~ N(40, 5^2)
P(X>=50) = 1 - P(X<50) = 1 - NORM.DIST(50, 40, 5, 1) - 예) 60만명이 수학능력시험을 봄, 평균 mean =220, 표준편차 sd =30 정규분포를 따름,
250점 학생은 몇등? (몇등? 이냐고 했으니 누적분포 사용해야 함)
P(X>=250) = 1 - P(X<=250) = `1 - pnorm(250, 220, 30)`
상위 10% 학생은 몇 점 정도인가? -> 밑에서 부턴 90%에 해당
P(X>=x) = 0.1 == P(X<=x) = 0.9
아래서 부터 퍼센트에 해당되는 문제 -> NORM.INV(궁금한 비율, 평균, 표준편차)
-> x값이 나오면 NORM.DIST 에 넣으면 다시 0.9 확인 가능
표준 정규분포표 Z ~ N(0,1) 일 때, P(Z<=0.11) 구하기
- pnorm(궁금한 범위, mean, sd)
pnorm(0.11, 0, 1)
728x90
'공부중 ...' 카테고리의 다른 글
| 데이터를 시각화하는 것이란 ... (0) | 2023.05.29 |
|---|---|
| 기댓값과 분산을 알아보자 (0) | 2023.05.17 |
| 이산형 확률분포에 대해서... 이항분포랑 포아송분포 (0) | 2023.04.25 |
| 시계열의 시간에 따른 의존관계, 자기상관 (1) | 2023.04.17 |
| 시계열의 주파수 분석과 확률과정에 대해서 (0) | 2023.04.16 |



